- Generals
HLA is an assembly language yes but its current implementation is as a compiler. It translates the HLA source code to HLA, masm, fasm. tasm or gas and use the appropriate assembler to transtate the assembly code to object code.
High-Level Assembly (HLA, MASM, TASM) is a proven operations strategy that allows OEMs to focus its in-house efforts on the top-level assembly to simplify production, minimize inventory, floor space, manufacturing overhead and direct labor(
IF/WHILE/FOR etc)
Often, for companies that serve cyclical markets, such as semiconductor equipment and alternative energy, shifting control to the contract manufacturers and utilizing a high-level assembly strategy allows companies to control fixed costs in an upturn and preserve a lower breakeven point in a down turn.
- Numberic representation
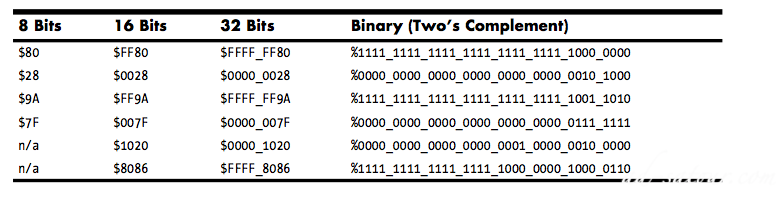
Nibble (4 bits), Word 16, Dword 32, Quard Word(64), Long word for 128-bit, tbyte(ten bytes, 80 bits)Sign extension(extend HO bit)
For example, to sign extend an 8-bit number to a 16-bit number, simply copy bit seven of the 8-bit number into bits 8..15 of the 16-bit number. To sign extend a 16-bit number to a double word, simply copy bit 15 into bits 16..31 of the double word.
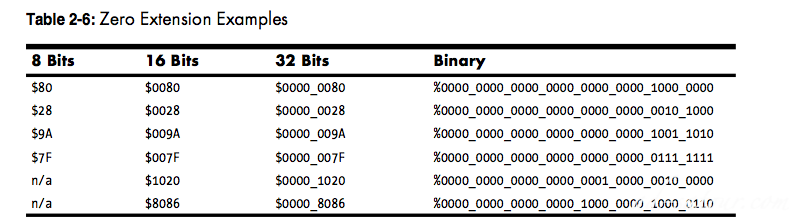
Zero extension(fill HO with zeros) === Sign extension with Zero
Sign contraction(all HO bits should be the same 0 or 1)
Sign contraction, converting a value with some number of bits to the same value with a fewer number of bits
To properly sign contract one value to another, you must look at the HO byte(s) that you want to discard.
First, the HO bytes must all contain either zero or $FF. If you encounter any other values, you cannot sign contract the value. Second, the HO bit of your resulting value must match every bit you’ve removed from the number.
Contraction:
Some language like C : will simply store the LO portion of the expression into a smaller variable and throw away the HO componentMay lost precision or real valueSaturation(ex:16bit to 8 bit, if −128..+127 -> copy LO, else store -128 or + 127 max)
Binary-Coded Decimal (BCD)( nibble nibble etc for decimal representation)
Ex: 35710 = 0011 0101 0111
(BCD)
Adv:
Standard binary floating point representationsTo display directly, especially system without microprocessor.Encoding and Decoding into BCD is easy.Hardware Algorithms (procedures) are east to implement on BCD codes.Scaling by a factor of 10 (or a power of 10) is simple
Inc:
Waste of memory
Fixed-Point Representation:
It’s usually more cost effective to use the CPU’s native floating-point format.Certain 3D gaming applications, for example, may produce faster computations using a 16:16 (16-bit integer, 16-bit fractional) format rather than a 32-bit floating-point format. Because there are some very good uses for fixed- point arithmetic.
Fractional values fall between zero and one, and positional numbering systems represent fractional values by placing digits to the right of the radix point
For example to represent 5.25: 1 × 22 + 1 × 20 + 1 × 2-2 = 4 + 1 + 0.25 = 5.25 In a 32-bit fixed-point format, this leaves either 21 or 22 bits for the fractional part, depending on whether your value is signed.
Fixed-point using BCD representation: (decimal fixed-point format)
33,44 coded in 4Xnibbles = 4X4= 16 bits (1 word)The binary format lets you exactly represent 256 different fractional values, whereas the BCD format only lets you represent 100 different fractional values.the only time the decimal fixed-point format has an advantage is when you commonly work with the fractional values that it can exactly represent(monetary)
Scaled Numeric Formats :
For example, if you have the values 1.5 and 1.3, their integer conversion produces 150 and 130. If you add these two values you get 280 (which corresponds to 2.8).When you need to output these values, you simply divide them by 100 and emit the quotient as the integer portion of the value and the remainder (zero extended to two digits, if necessary) as the fractional component.When doing addition or subtraction with a scaled format, you must ensure that both operands have the same scaling factor.
Rational Representation:
One integer represents the numerator (n) of a fraction, and the other represents the denominator (d). The actual value is equal to n/d.
- Binary Arithmetic and Bit Operations:
Multiplying two n-bit binary values together may require as many as 2*n bits to hold the result.Adding or subtracting two n-bit binary values never requires more than n+1 bits to hold the result.Division and multiplication in Binary more easy than other representations.Masking bit strings: %0000_1111(8) AND others
Useful Bit Operations:
Testing Bits in a Bit String Using AND: IsOdd = (ValueToTest & 1) != 0;Testing a Set of Bits for Zero/Not Zero Using AND: IsDivisibleBy16 := (ValueToTest and $f) = 0;Comparing a Set of Bits Within a Binary String: (value1 & 0x81010403) == (value2 & 0x81010403)
Creating Modulo-n Counters Using AND:
cntr = (cntr + 1 ) % n; => division is an expensive operation.cntr := cntr + 1; // Pascal example if( cntr >= n ) then cntr := 0;
if cntr is a power of 2
n = 2m−1ex: 32 => 0x3f=31=25 −1,so n=32 and m=5.cntr = (cntr + 1) & 0x3f;
Logical Shifts left and right:
cLang = d << 1; shift leftShifting all the bits in a number to the left by one position multiplies the binary value by two. the multiplication operation is usually slower than the shift left operation. when we shift right we divide by two. only unsigned
Arithmetic shift left/right:
To divide a signed number by two using a shiftArithmetic left shift = Logical left shiftArithmetic right shift: sign bit is kept at leftIn java The operators << (left shift), >> (signed right shift), and >>> (unsigned right shift) are called the shift operators.
Rotation:
Rotate instructions that recirculate bits through an operand by taking the bits shifted out of one end of the operation and shifting them into the other end of the operand.Rotate through carry is especially useful when performing shifts on numbers larger than the processor’s native
Bit Fields and Packed Data(in C lang, structure) (packed to YYYYMMDD, MMMMDDDDDYYYYYYY), but unpacking:
space efficientcomputationally inefficient(slow)
Long packed date format: Year (0-65535) Month (1-12) Day (1-31)
Long spaceComputationally efficient(because written in bytes, so easy to compare etc)
- Floating
Floating
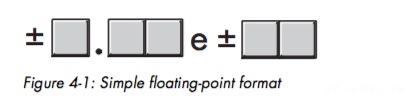
The first issue: dynamic range.In a floating-point value, the radix point (binary point) can freely float between digits in the number as neededOne additional field — a field that specifies the position of the radix point within the number. This extra field is equivalent to the exponent present when using scientific notation.Most floating-point formats use some number of bits to represent a mantissa and a smaller number of bits to represent an exponent.Mantissa fall between a fixed range(ex: 0 and 1)The exponent: The exponent is a multiplier that when applied to the mantissa produces values outside this range3 significant digits, 2 exponent digits
Incv: a form of scientific notation, complicatesarithmetic somewhat. When adding and subtracting two numbers in scientific notation, you must adjust the two values so that their exponents are the same=> round or truncate result => Lack of precision => affect accuracyGuard digits(extra digit to add more precision with calculations)
The order of evaluation can affect the accuracy of the result.
FPUs or floating-point software packages might actually insert random digits (or bits) into the LO positionWhen multiplying and dividing sets of numbers, try to multiply and divide num- bers that have the same relative magnitudes.
Accuracy
FPUs or floating-point software packages might actually insert random digits (or bits) into the LO positionThe order of evaluation can affect the accuracy of the result.Multiplication and division first then addition and subtractionWhen multiplying and dividing sets of numbers, try to multiply and divide numbers that have the same relative magnitudes.
Scientific notation, complicates arithmetic somewhat:
So we must either round or truncate the result to three significant digitsThe lack of precision => affect accuracyExtra digits are known as guard digits (or guard bits in the case of a binary format).They greatly enhance accuracy during a long chain of computations.
Compare:
The test for equality succeeds if and only if all bits (or digits) in the two operands are the sameThe standard way to test for equality between floating-point numbers is to determine how much error (or tolerance) you will allow in a comparisonWhen comparing two floating-point numbers for equality, always compare the values to see if the difference between two values is less than some small error value.Miserly approach to comparing for less than or greater than (that is, we try to find as few values that are less than or greater than as possible).An eager approach attempts to make the result of the comparison true as often as possible: if( A < (B + error)) then Eager_A_lessthan_B;
IEEE Floating-Point Formats: IEEE 754
Single, double, extended precision
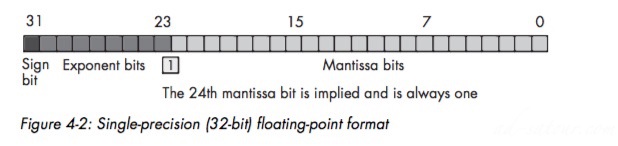
Single-precision floating-point format:
24 bits mantissa, and 8 bit exponent1.0 <= Mantissa < 2.0The HO bit of mantissa is always 1: 1.mmmmmm mmmmm mmmmmm6 to 9 decimal digits, about 7 on averageMantissa use one’s complement format rather than two’s
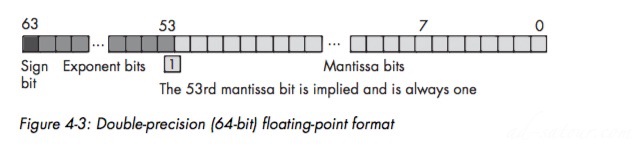
Double-Precision Floating-Point Format
15 to 17 decimal digits, about 16 on average
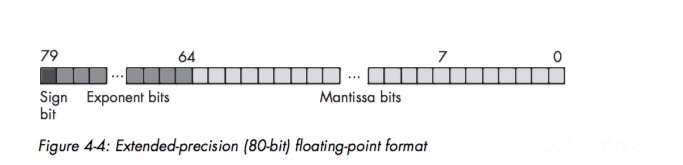
Extended-Precision Floating-Point Format:
The extended-precision format uses 80 bits.
On the 80×86 FPUs, all computations are done using the extended-precision form. Whenever you load a single- or double-precision value, the FPU auto- matically converts it to an extended-precision value
Normalization and denormalized values
A normalized floating-point value is one whose HO mantissa bit contains one.
Benefit maintaining high precision; If HO bits has all zero => fewer bits of precision.
Unnormalized to normalized => left shifting and decrementing the exponent until a one appears in HO bit of the mantissa.Exponent is a binary exponent => incrementing leads to multiply the floating-point value by 2.The IEEE floating-point formats use all zero bits in the exponent and mantissa fields to denote the value zeroWe keep using denormalized (for precisions) when: Mantissa with a lot of Zero bits, exponent with 0
Rounding
A result with greater precision than the floating-point format supports (the guard bits in the calculation maintain this extra precision)
Types of rounding:
Truncation: Conversion from Float-point value to integersRounding up: Ceil(rounds a floating-point value to the smallest possible larger integer)Rounding down: Floor(the largest possible smaller value)Rounding to the nearest:
Special floating-point values:
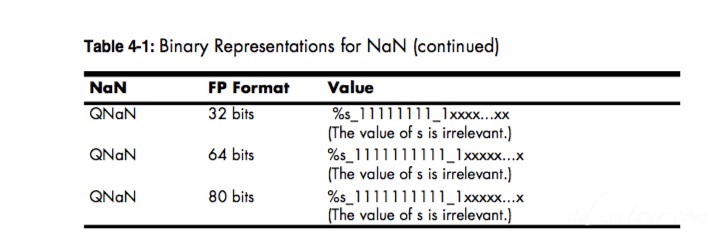
An exponent containing all one or zero bits indicates a special valueQNaN represent indeterminate results : quiet not-a-number
SNaN specify that an invalid operation has taken place: signaling not-a-number
Two other special values are represented when the exponent contains all one bits, and the mantissa contains all zeros.
In such a case, the sign bit determines whether the result is the representation for +infinity or −infinity.
Floating-Point Exceptions:
Invalid operationDivision by zero Denormalized operandNumeric overflow Numeric underflow Inexact result
- Character representation
Character data
ASCII
American Standard Code for Information Interchange$0..$1F: Control characters.
$30..$39: Punctuation symbols, special characters, and the numeric digits.
$30 = 0 ASCII, $31 = 1, etc$41..$5A: Uppercase alphabets, starting with A.$61..$7A: Lowercase alphabets, starting with a.A to a ASCII => Change bit 5 from 0 to 1.
End-of-line: Carriage return, Line Feed.
CR/LF:(2 characters) for Windows, MS-DOS etcCR: MacLF: Linux/Unix
EBCDIC
Extended Binary Coded Decimal Interchange Code. Extended from BCDIC
DBCSs
Double-byte character sets.They use a single byte for most character encodings and use two- byte codes only for certain characters.A typical double-byte character set utilizes the standard ASCII character set along with several additional characters in the range $80..$FF
Unicode Character Set
Unicode uses a 16-bit word to represent each character.Unicode supports up to 65,536 different character codes.If the HO 9 bits3 of a Unicode contains 0, then the LO 7 bits use the ASCII.
Character String
Attributes
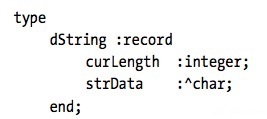
Possesses two main attributes: a length and the character dataMaybe other attributes: Max length, reference count:number of variables refer to the same String.
Character String Formats
Most languages use data strutures
Zero-Terminated Strings:
Most common representation, native string format for C, C++, Java.It’s a sequence containing zero or more 8-bit character codes ending with a byte containing zero.Or, in the case of Unicode, a sequence containing zero or more 16-bit character codes ending with a 16-bit word containing zero.For example, in C/C++, the ASCII string “abc” requires four bytes
Length-Prefixed Strings
Common like in PascalSingle Length Byte + Zero or more 8-bit character codes.”abc” = $03abc
Solve 2 problems:
Possible to represent NUL characterOperations are more efficient.
Limited to 255 characters in length.
Other uses 2-4 byte length value.
Seven-Bit Strings
Use ASCII 7-bit codes.HO to indicate the end of the string.The last character HO should be clear.
Incv:
No zero-length String.Limited to 128 character codes.
HLA Strings
Costs nine bytes of overhead per string
4 byte extra informations( overhead)4 byte length prefix0 Byte at the end
Descriptor-Based Strings
String record structure, called descriptors
Possibility to add many fields: Max length, etc.
Types of Strings: Static, Pseudo-Dynamic, and Dynamic:
Static Strings
Max size is predeterminated by programmer: ex: var pascalString :string(255)ex: char cString[256]While the program is runing there is no way to increase the max size, neither to reduce it.
Pseudo-Dynamic Strings
Pseudo-dynamic strings are those whose length the system sets at run time by calling a memory-management function like malloc to allocate storage for the string.However, once the system allocates storage for the string, the maximum length of the string is fixed.
Dynamic-Strings
Dynamic string systems, which typically use a descriptor-based format, will automatically allocate sufficient storage for a string object whenever you create a new string or otherwise do something that affects an existing string.Copy on write. Whenever a string function needs to change some characters in a dynamic string, the function first makes a copy of the string and then makes whatever modifications are necessary to the copy of the dataTo avoid a memory leak, dynamic string systems employing copy-on-write usually provide garbage collection code that scans through the string area looking for stale character data in order to recover that memory for other purposes
Reference Counting for Strings:
A reference counter is an integer that counts the number of pointers that reference a string’s character data in memory. Deallocation of the storage for the actual character data doesn’t happen until the reference counter decrements to zero. Delphi/Kylix Strings
- Memory Organization and Access
The Basic System Components
The 80×86 family uses the von Neumann architecture (VNA): Central processing unit (CPU), memory, and input/output (I/O)The System Bus: Most CPUs have three major buses: the address bus, the data bus, and the control bus
Data Bus:
CPUs use the data bus to shuffle data between the various components The size of this bus varies widely among CPUsBus size is one of the main attributes that defines the “size” of the processor( 32-bit-wide or 64-bit-wide)Modern Intel 80×86 CPUs all have 64-bit buses, but only pro- vide 32-bit general-purpose integer registers, so we’ll classify these devices as 32-bit processors. The AMD x86-64 processors support 64-bit integer registers and a 64-bit bus, so they’re 64-bit processors
Address Bus:
The data bus on an 80×86 family processor transfers information between a particular memory location or I/O device and the CPUWith a single address bus line, a processor could access exactly two unique addresses: zero and oneWith n address lines, the processor can access 2n unique addresses80x86 processors provides 20 lines
Control Bus:
The control bus is an eclectic collection of signals that control how the processor communicates with the rest of the systemLines: read and write: CPU to memory, or memory to CPUClock lines, interrupt lines, byte enable lines, and status lines
Physical Organization of Memory
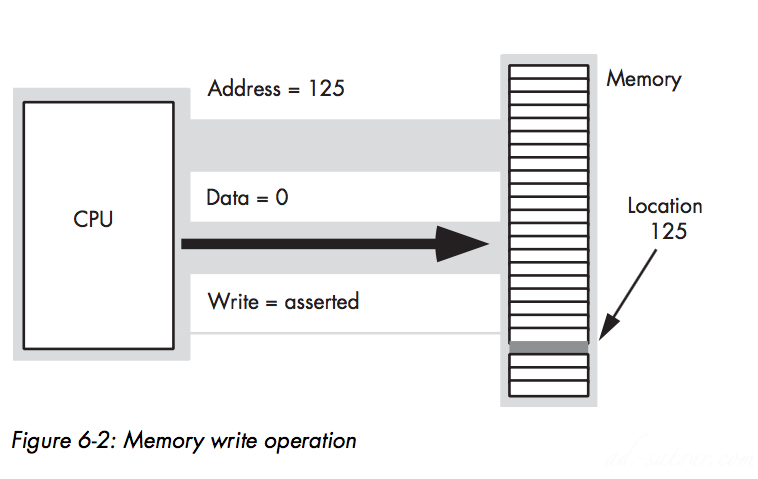
CPU := Memory [125]; Memory [125] := 0;
For Larger than eight bits:
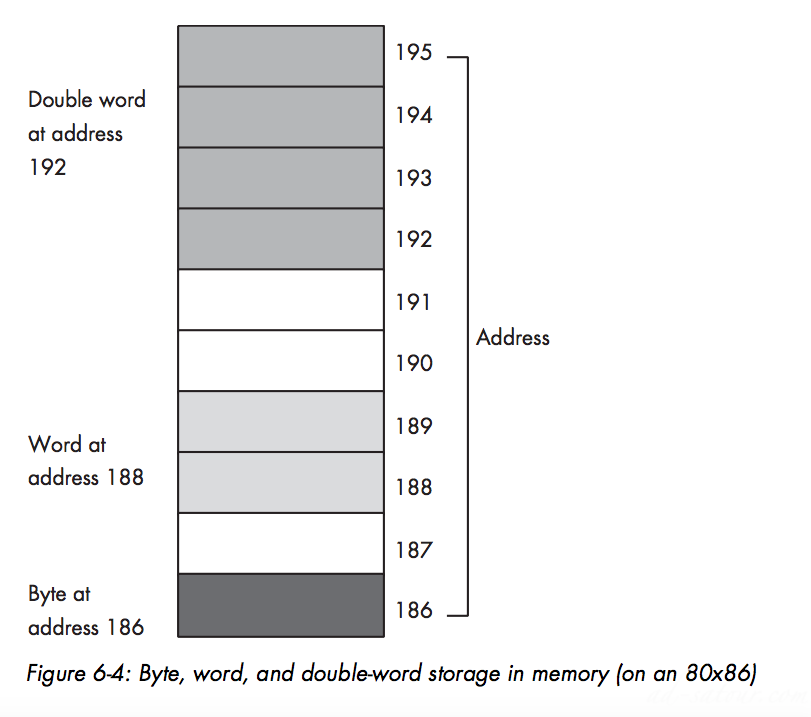
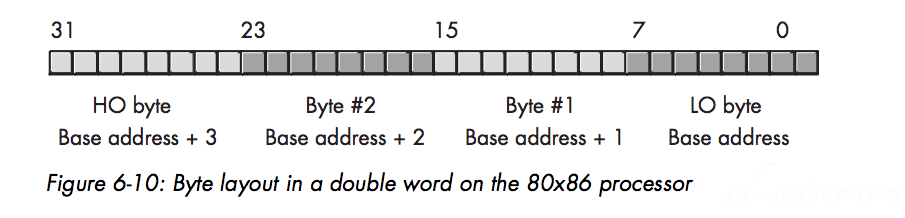
The 80×86 family stores the LO byte of a word at the address specified and the HO byte at the next location Therefore, a word consumes two consec- utive memory addresses
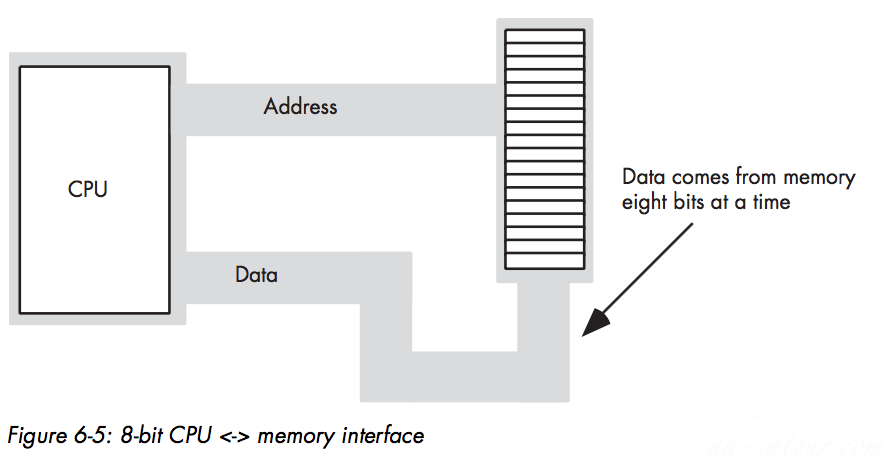
8-Bit Data Buses:
A processor with an 8-bit bus (like the old 8088 CPU) can transfer 8 bits of data at a time Because each memory address corresponds to an 8-bit byte
The term byte-addressable memory array means that the CPU can address memory in chunks as small as a single byteIt also means that this is the smallest unit of memory you can access at once with the processor. That is, if the processor wants to access a 4-bit value, it must read eight bits and then ignore the extra four bits.Addresses are integers
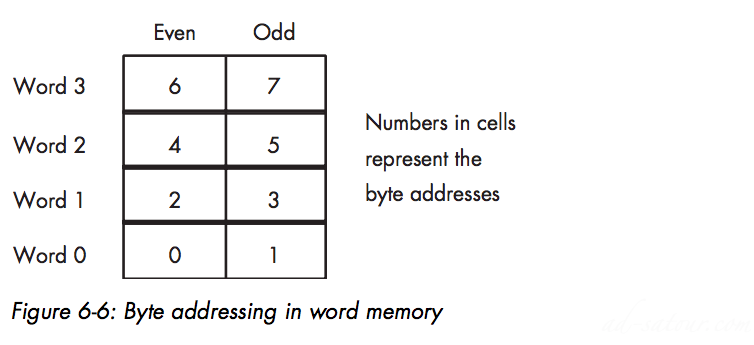
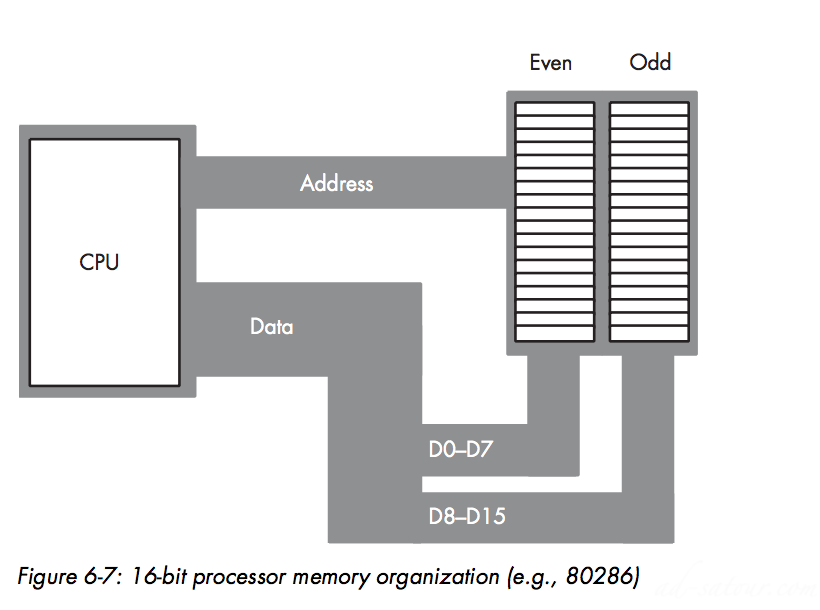
16-Bit Data Buses:
Byte Addressing in word memory
If you access a single byte, the CPU activates the appropriate bank (using a byte-enable control line) and transfers that byte on the appropriate data lines for its address.So accessing words at odd addresses on a 16-bit processor is slower than accessing words at even addresses(Swap)
32-Bit Data Buses
32-bit processor memory interface
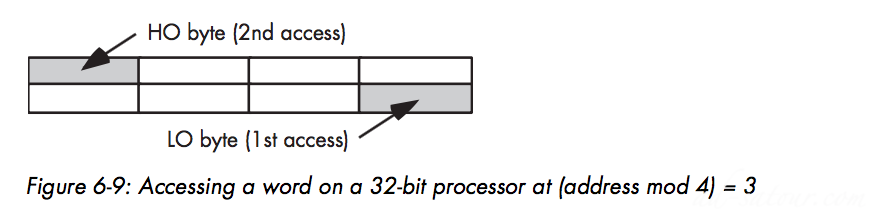
With a 16-bit memory interface the address placed on the address bus is always an even number, and similarly with a 32- bit memory interface, the address placed on the address bus is always some multiple of fourUsing various byte-enable control lines, the CPU can select which of the four bytes at that address the software wants to access.2 memory operations
A 32-bit CPU can access a double word in a single memory operation only if the address of that value is evenly divisible by four. If not, the CPU may require two memory operations.
64-Bit Buses
The Pentium and later processors provide a 64-bit data bus and special cache memory that reduces the impact of nonaligned data access. Although there may still be a penalty for accessing data at an inappropriate address, modern x86 CPUs suffer from the problem less frequently than the earlier CPUs.
Big Endian Versus Little Endian Organization
Little endian byte organization
ex: Intel
Big endian byte organization: Mac, Unixbyte genders
Struct and Union:
Unions, they are a data structure similar to records or structs except the compiler allocates the storage for each field of the union at the same address in memoryStruct vs Union:
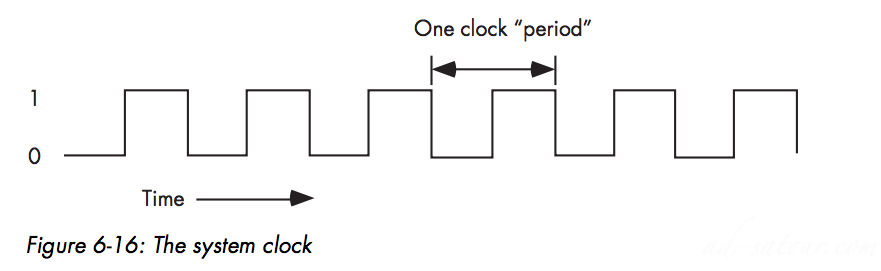
The System Clock
The system clock is an electrical signal on the control bus that alternates between zero and one at a periodic rate
A CPU running at 1 GHz would have a clock period of one nanosecond (ns)To ensure synchronization, most CPUs start an operation on either the falling edge (when the clock goes from one to zero) or the rising edge (when the clock goes from zero to one)Because all CPU operations are synchronized with the clock, the CPU cannot perform tasks any faster than the clock runs.
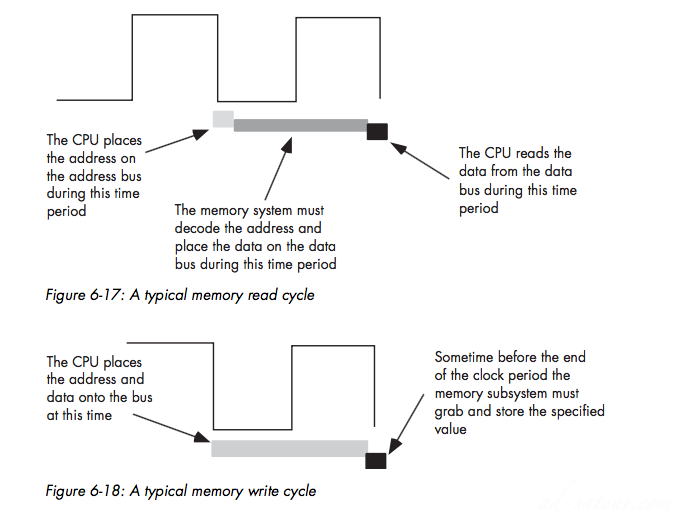
Memory Access and the System Clock
Memory access occurs no more often than once every clock cycleThe memory access time is the number of clock cycles between a memory request (read or write) and when the memory operation completesRead Write Cycle
Wait States
A wait state is an extra clock cycle that gives a device additional time to respond to the CPU
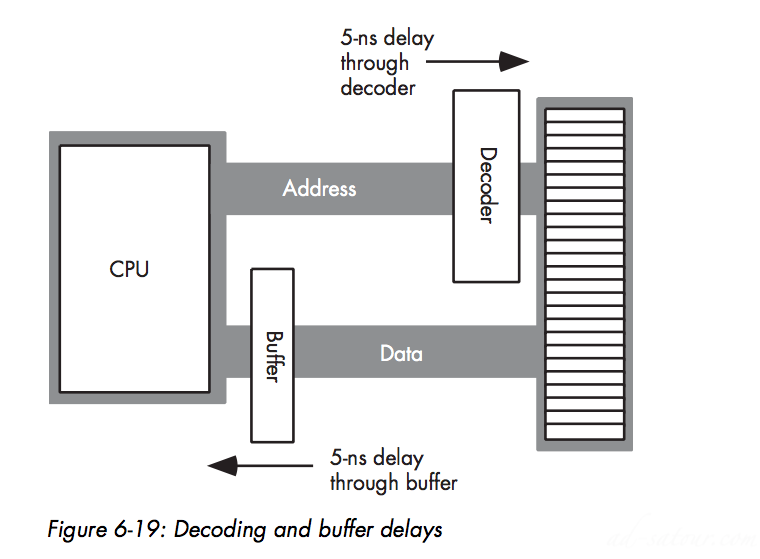
However, we’re not doomed to slow execution because of added wait states. There are several tricks hardware designers can employ to achieve zero wait states most of the time. The most common of these is the use of cache (pronounced “cash”) memory.
Cache Memory
If you look at a typical program, you’ll discover that it tends to access the same memory locations repeatedly. Furthermore, you’ll also discover that a program often accesses adjacent memory locationsThe technical names given to these phenomena are temporal locality of reference and spatial locality of reference.
Loop for example:
A cache hit occurs whenever the CPU accesses memory and finds the data in the cache. In such a case, the CPU can usually access data with zero wait statesA cache miss occurs if the data cannot be found in the cache. In that case, the CPU has to read the data from main memory, incurring a performance lossTo take advantage of temporal locality of reference, the CPU copies data into the cache whenever it accesses an address not present in the cache.
CPU Memory Access
Introduction:
Common memory addressing modes: direct, indirect, indexedAdditional addressing modes: scaled indexedA particular addressing mode can allow to access data in a complex data structure with a single instructio
The Direct Memory Addressing Mode
The direct addressing mode encodes a variable’s memory address as part of the actual machine instruction that accesses the variable.
Direct addresses are 32-bit values appended to the instruction’s encodingA program uses the direct addressing mode to access global static variables
The Indirect Memory Addressing Mode
Uses a register to hold a memory address :
Adv:
You can modify the value of an indirect address at run time Encoding register (the indirect address) takes far fewer bits than encoding a 32-bit (or 64-bit) direct address, so the instructions are smaller
Incv:
Take one or more instructions to load a register with an addressThe indirect addressing mode is useful for many operations, such as accessing objects referenced by a pointer variable.
The Indexed Addressing Mode
The indexed addressing mode combines the direct and indirect addressing modes into a single addressing mode
Optimized instruction in some CPU
Encode both an offset (direct address) and a register in the bits that make up the instructionAt run time, the CPU computes the sum of these two address components to create an effective addressThe byteArray[ebx] instruction in this short program demonstrates the indexed addressing mode. The effective address is the address of the byteArray variable plus the current value in the EBX register.This addressing mode is great for accessing array elements and for indirect access to objects like structures and records
The Scaled Indexed Addressing Modes:
The ability to use two registers (plus an offset) to compute the effective addressThe ability to multiply one of those two registers’ values by a common constant (typically 1, 2, 4, or 8) prior to computing the effective address.Adv: This addressing mode is especially useful for accessing elements of arrays whose element sizes match one of the scaling constants
- Composite Data Types and Memory Objects
Pointer Types
A pointer is a variable whose value refers to some other object
Pointer Implementation
Most languages implement pointers using memory addresses, a pointer is actually an abstraction of a memory address
Double indirection pointer:
Because double indirection requires 50 percent more code than single indirection, you can see why many languages implement pointers using single indirection.
Pointers and Dynamic Memory Allocation
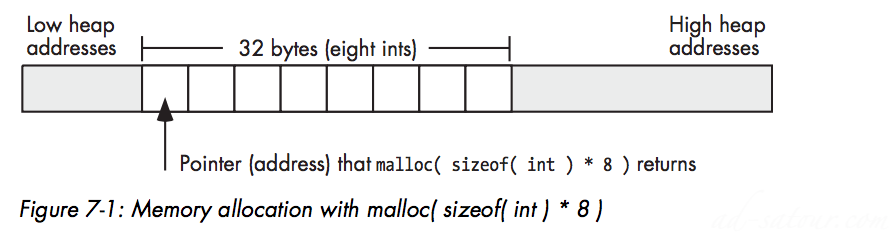
Heap: a region in memory reserved for dynamic storage allocationPointers typically reference anonymous variables that you allocate on the heap using memory allocation/deallocation functions in different languages like malloc/free (C), new/dispose (Pascal), and new/delete (C++)Objects you allocate on the heap are known as anonymous variables because you refer to them by their address, and you do not associate a name with them
Pointer Operations and Pointer Arithmetic
The pointer data type let you assign addresses to pointer variables, compare pointer values for equality or inequality, and indirectly reference an object via a pointer.ptrVar = malloc( bytes_to_allocate );ptrVar = malloc( sizeof( int ) * 8 );
Adding an Integer to a Pointer
in the C/C++ language you can indirectly access objects in memory using an expression like *(p + i) (where p is a pointer to an object and i is an integer value)
Subtracting an Integer from a Pointer
mov( [ebx−4], eax ); *(p − i)
Subtracting a Pointer from a Pointer
Now compute the number of characters between the ‘a’ and the ‘e’ // (counting the ‘a’ but not counting the ‘e’): distance = (ePtr – aPtr);
Comparing Pointers:
Such a comparison will tell you whether the pointers reference the same object in memory
Arrays
Introduction
After strings, arrays are probably the most common composite data type (a complex data type built up from smaller data objects)Abstractly, an array is an aggregate data type whose members (elements) are all of the same typeMemory Representation
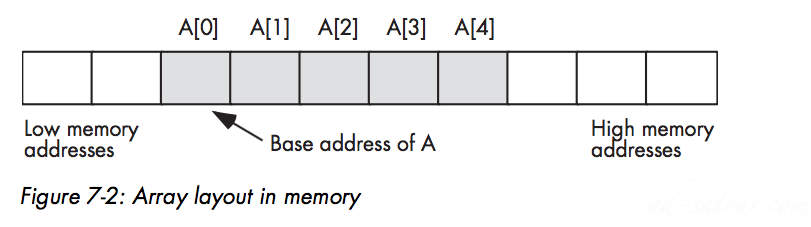
The base address of an array is the address of the first element of the array and is at the lowest memory location.
Array Declarations
data_type array_name [ number_of_elements ];data_type array_name[ number_of_elements ] = {element_list};
Array Representation in Memory
Representation
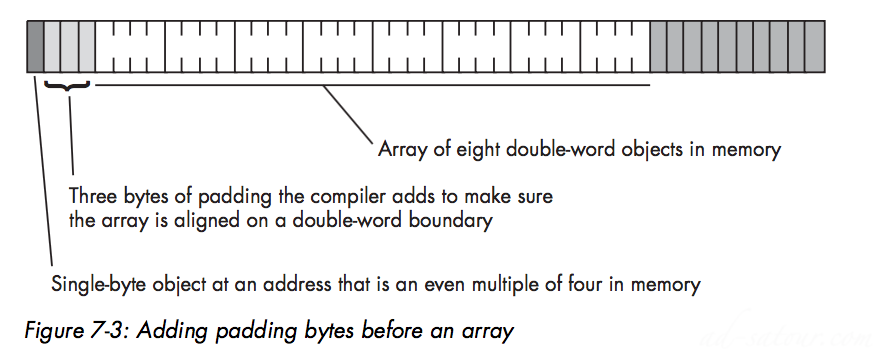
If the size of each array element is less than the minimum size memory object the CPU supports, the compiler implementer has two options:
Allocate the smallest accessible memory object for each element of the array
Adv: FastIncv:Wastes memory
Pack multiple array elements into a single memory cell
Adv: Compact, Incv: Requires extra instructions to pack and unpack data when accessing array elements, which means that accessing elements is slower
Accessing Elements of an Array
Element_Address = Base_Address + index * Element_Size Ex: var SixteenInts : array[ 0..15] of integer; Element_Address = AddressOf( SixteenInts) + index*4 Ex Assembly: mov( index, ebx ); mov( SixteenInts[ ebx*4 ], eax );
Multidimensional Arrays
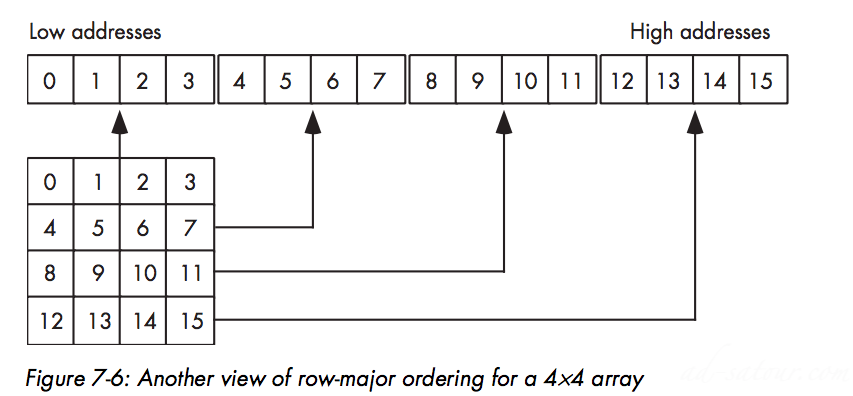
There are two functions that most HLA use: row-major ordering and column-major ordering.
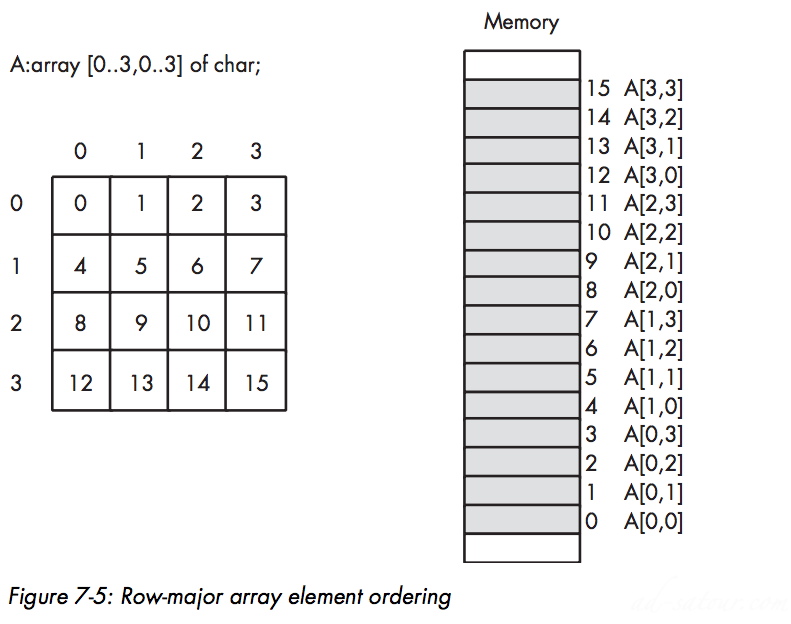
Row-Major Ordering
C/C++, Java, Ada use itHow
Another view of memory
Element_Address = Base_Address + (colindex * row_size + rowindex) * Element_Size
Base_Address is the address of the first element of the array (A[0][0] in this case)
For 3 dimension:
dataType[depth_size][col_size][row_size];Address = Base + ((depth_index * col_size + col_index)*row_size + row_index) * Element_Size
Column-Major Ordering
FORTRAN, Basic etc
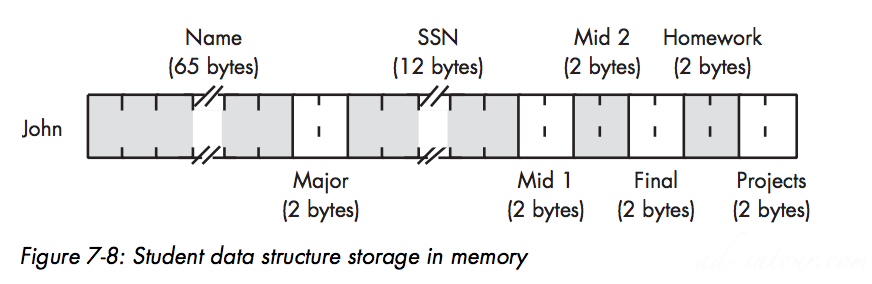
Records/Structures
Introduction
An array is homogeneous, meaning that its elements are all of the same type. A record, on the other hand, is heterogeneous and its elements can have differing types.Records in C/C++
Memory Storage of Records
Memory representation
Padding to multiple of 4 :
Many of these compilers also provide a pragma or a packed keyword of some sort that lets you turn off field alignment on a record-by-record basis.Disabling alignment: save memory but against time(more slower)
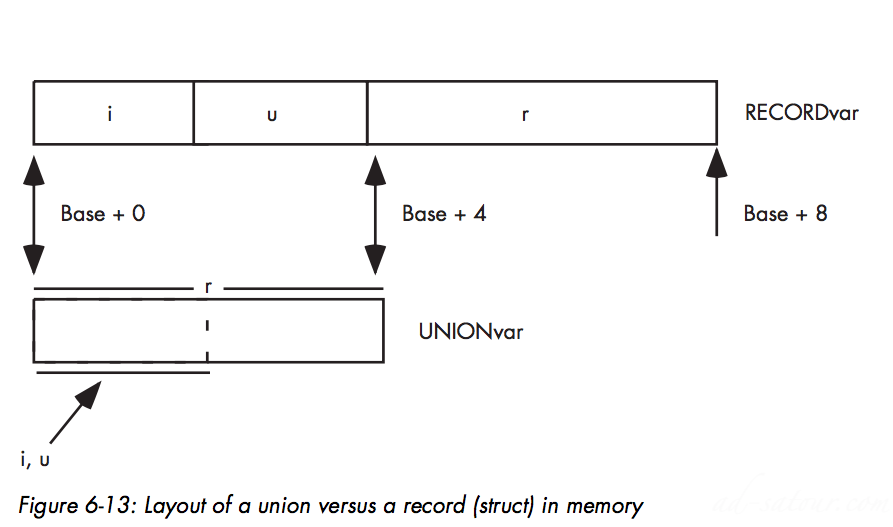
Discriminant Unions
A discriminant union (or just union) is very similar to a recordIn a record, each field has its own offset from the base address of the record, and the fields do not overlap. In a union, however, all fields have the same offset, zero, and all the fields of the union overlapSize of Record = Sum of all the fields size + maybe padding bytesSize of Union = The size of it’s largest field + maybe padding
- Boolean Logic and Digital Design
Generalities
Any program you can write, you can also specify as a sequence of Boolean equations(Hardware)
Boolean Operator Precedence
parentheses logical NOTlogical AND logical OR
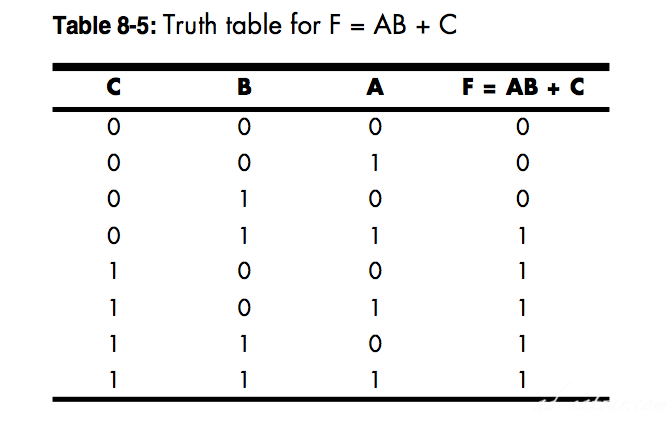
Boolean Functions and Truth Tables
Given n input variables, there are 22^n unique Boolean functions (3 gives 256 functions)
Function Numbers
Truth table for F = AB + C
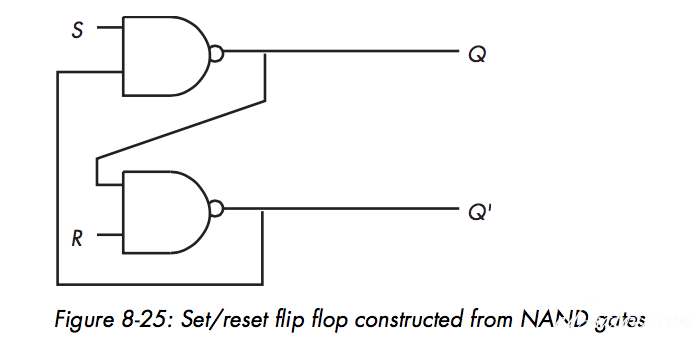
The Set/Reset Flip-Flop
How to remember result, memory cell
- CPU Architecture
Basic CPU Design
The control unit( CU) uses a special register, the instruction pointer, that holds the address of an instruction’s numeric code (also known as an operation code or opcode).The control unit fetches this instruction’s opcode from memory and places it in the instruction decoding register for execution. After executing the instruction, the control unit increments the instruction pointer and fetches the next instruction from memory for execution. This process repeats for each instruction the program executes.
Decoding and Executing Instructions: Random Logic Versus Microcode
A hardwired, or random logic,2 approach uses decoders, latches, counters, and other hardware logic devices to operate on the opcode data. The microcode approach involves a very fast but simple internal processor that uses the CPU’s opcodes as indexes into a table of operations called the microcode, and then executes a sequence of microinstructions that do the work of the macroinstruction they are emulating.CPUs based on microcode contain a small, very fast execution unitThe micro-engine itself is usually quite fast, the micro-engine must fetch its instructions from the microcode ROM (read-only memory)
Conclusion:
If memory technology is faster than CPU technology, the microcode approach tends to make more sense. If memory technology is slower than CPU technology, random logic tends to produce faster execution of machine instructions.
Executing Instructions, Step by Step
mov, add, loop, and jnz (jump if not zero)The mov instruction copies the data from the source operand to the destination operandThe add instruction adds the value of its source operand to its destination operandThe loop and jnz instructions are conditional-jump instructions — they test some condition and then jump to some other instruction in memory if the condition is true, or continue with the next instruction if the condition is false
The loop instruction decrements the value of the ECX register and transfers control to a target instruction if ECX does not contain zero (after the decrement). This is a good example of a Complex Instruction Set Computer (CISC) instruction because it does multiple operations:
It subtracts one from ECX.It does a conditional jump if ECX does not contain zero.
Parallelism — The Key to Faster Processing
How?
An early goal of the Reduced Instruction Set Computer (RISC) processors was to execute one instruction per clock cycle, on the averageBy overlapping various stages in the execution of these instructions, we’ve been able to substantially reduce the number of steps, and consequently the number of clock cycles, that the instructions need to complete execution
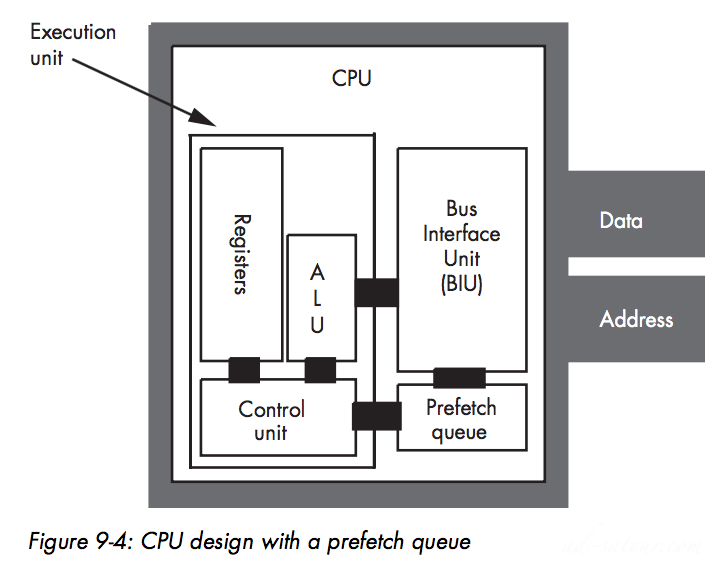
The Prefetch Queue:
Saving Fetched Bytes Using Unused Bus CyclesOverlapping Instructions
Conditions That Hinder the Performance of the Prefetch Queue
Because they invalidate the prefetch queue, jump and conditional-jump instructions are slower than other instructions when the jump instructions actually transfer control to the target locationIf you want to write fast code, avoid jumping around in your program as much as possible.
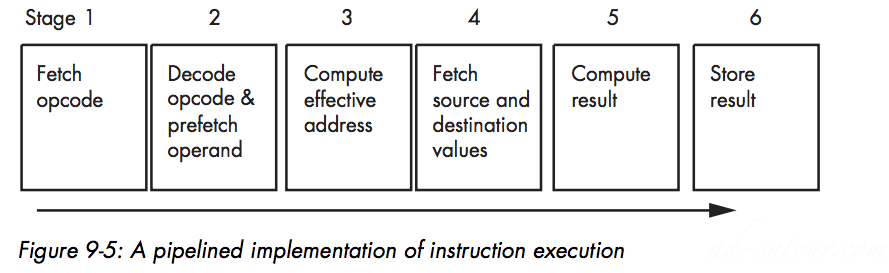
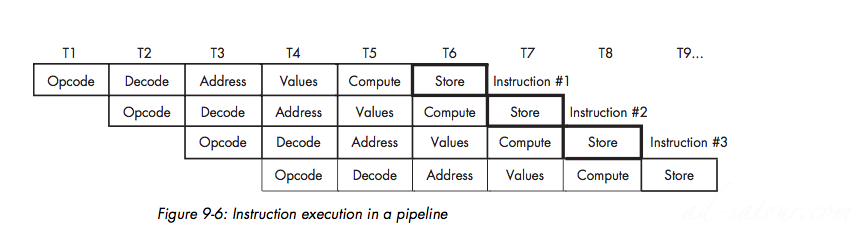
Pipelining — Overlapping the Execution of Multiple Instructions
A Typical Pipeline
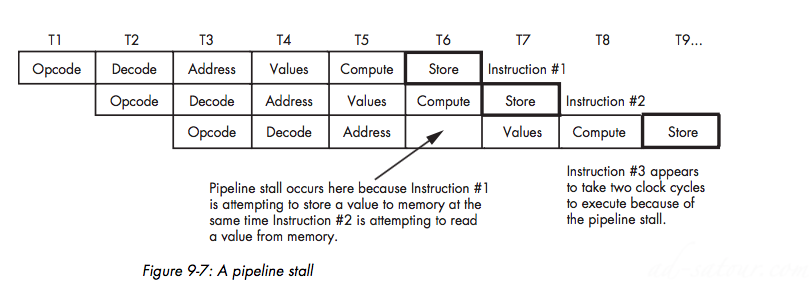
Stalls in a Pipeline
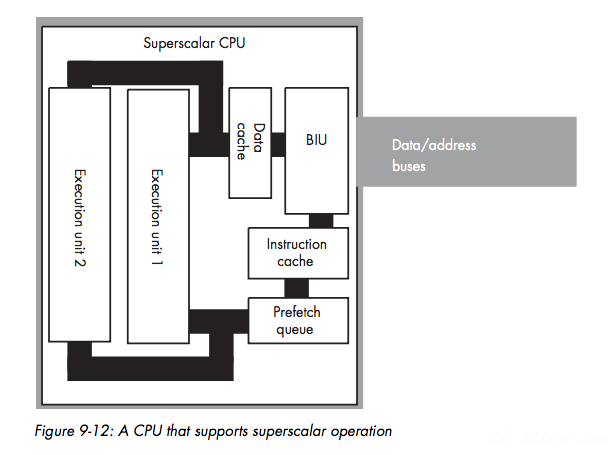
Instruction Caches — Providing Multiple Paths to MemoryPipeline HazardsSuperscalar Operation — Executing Instructions in Parallel
Out-of-Order ExecutionRegister RenamingVery Long Instruction Word (VLIW) ArchitectureParallel ProcessingMultiprocessing: Adding another CPU to the system









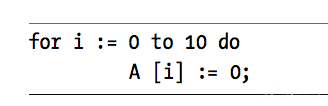














No Comments